Skip to main content

Water Tank 6Eq

System​

x˙0=u0+0.1+k1(4−x5)−k02gx0x˙1=k02g(x0−x1)x˙2=k02g(x1−x2)x˙3=k02g(x2−x3)x˙4=k02g(x3−x4)x˙5=k02g(x4−x5)\begin{align*} \dot{x}_{0} &= u_{0} + 0.1 + k_{1} (4 -x_{5}) - k_{0} \sqrt{2gx_{0}} \\ \dot{x}_{1} &= k_{0} \sqrt{2g (x_{0}-x_{1})} \\ \dot{x}_{2} &= k_{0} \sqrt{2g (x_{1}-x_{2})} \\ \dot{x}_{3} &= k_{0} \sqrt{2g (x_{2}-x_{3})} \\ \dot{x}_{4} &= k_{0} \sqrt{2g (x_{3}-x_{4})} \\ \dot{x}_{5} &= k_{0} \sqrt{2g (x_{4}-x_{5})} \end{align*}

where k0=0.015,k1=0.01,g=9.81k_{0} = 0.015, k_{1}= 0.01, g=9.81

Implementation​

import numpy as np
from pyrat.algorithm import ALTHOFF2013HSCC
from pyrat.dynamic_system import NonLinSys
from pyrat.geometry import Geometry, Zonotope
from pyrat.geometry.operation import cvt2
from pyrat.model import tank6eq
from pyrat.util.visualization import plot

# init dynamic system
system = NonLinSys(Model(tank6eq, [6, 1]))

# settings for the computations
options = ALTHOFF2013HSCC.Options()
options.t_end = 400
options.step = 4
options.tensor_order = 3
options.taylor_terms = 4
options.r0 = [Zonotope([2, 4, 4, 2, 10, 4], np.eye(6) * 0.2)]
options.u = Zonotope([0], [[0.005]])
options.u = Zonotope.zero(1, 1)
options.u_trans = np.zeros(1)

# settings for using geometry
Zonotope.REDUCE_METHOD = Zonotope.METHOD.REDUCE.GIRARD
Zonotope.ORDER = 50
Zonotope.INTERMEDIATE_ORDER = 50
Zonotope.ERROR_ORDER = 20

_, tp, _, _ = ALTHOFF2013HSCC.reach(system, options)

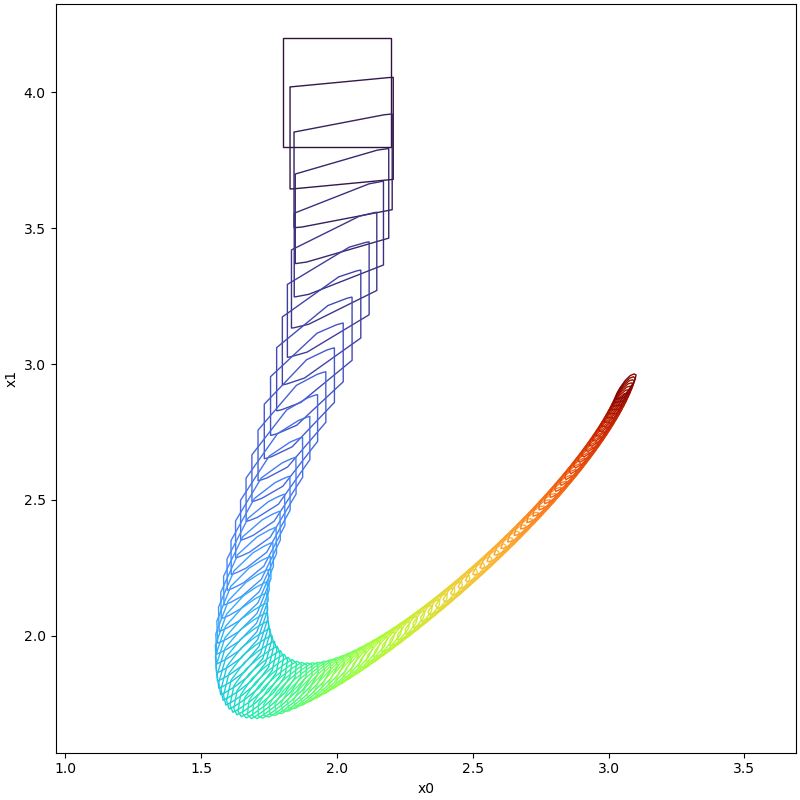
plot(tp, [0, 1])
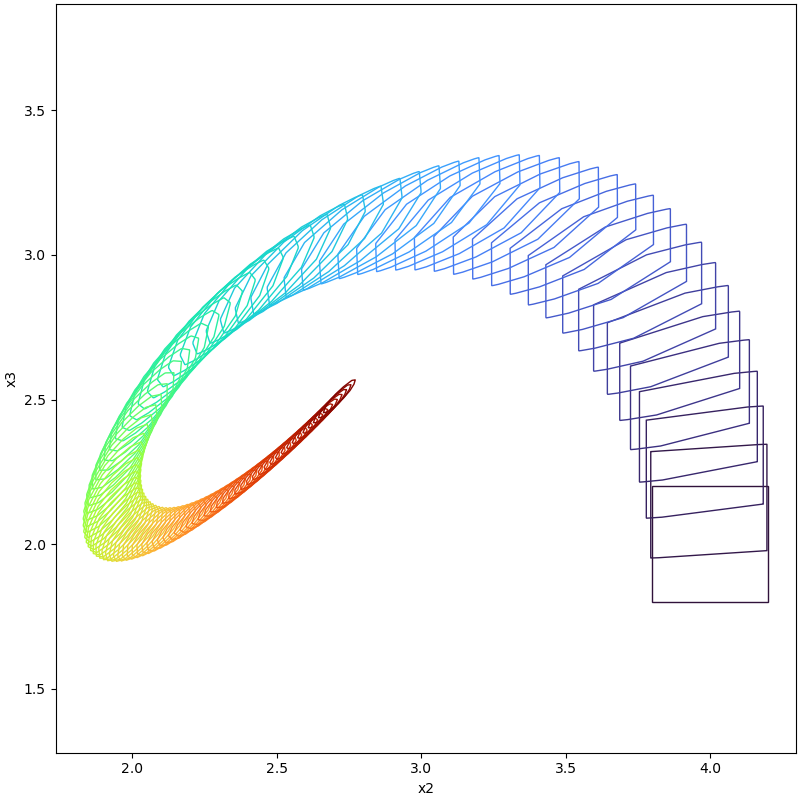
plot(tp, [2, 3])
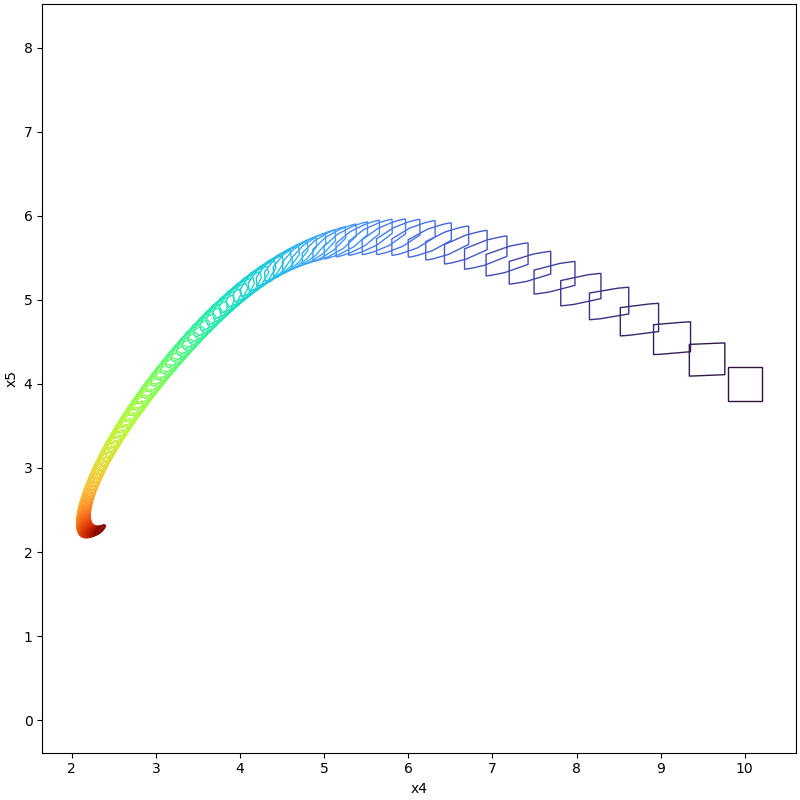
plot(tp, [4, 5])

Results​