Skip to main content

Laub Loomis

System​

x˙0=1.4x2−0.9x0x˙1=2.5x4−1.5x1x˙2=0.6x6−0.8x1x2x˙3=2−1.3x2x3x˙4=0.7x0−x3x4x˙5=0.3x1−3.1x5x˙6=1.8x5−1.5x1x6\begin{align*} \dot{x}_{0} &= 1.4 x_{2} - 0.9 x_{0} \\ \dot{x}_{1} &= 2.5 x_{4} - 1.5 x_{1} \\ \dot{x}_{2} &= 0.6x_{6} - 0.8 x_{1} x_{2} \\ \dot{x}_{3} &= 2 - 1.3 x_{2} x_{3} \\ \dot{x}_{4} &= 0.7 x_{0} - x_{3}x_{4} \\ \dot{x}_{5} &= 0.3 x_{1} - 3.1 x_{5} \\ \dot{x}_{6} &= 1.8 x_{5} - 1.5 x_{1} x_{6} \end{align*}

Implementation​

# init dynamic system
system = NonLinSys.Entity(LaubLoomis())

# settings for the computation
options = ASB2008CDC.Options()
options.t_end = 20
options.step = 0.04
options.tensor_order = 2
options.taylor_terms = 4
options.r0 = [Zonotope([1.2, 1.05, 1.5, 2.4, 1, 0.1, 0.45], np.eye(7) * 0.01)]
options.u = Zonotope([0], [[0.005]])
options.u = Zonotope.zero(1, 1)
options.u_trans = np.zeros(1)

# settings for using geometry
Zonotope.REDUCE_METHOD = Zonotope.METHOD.REDUCE.GIRARD
Zonotope.ORDER = 50

tps = ASB2008CDC.reach(system, options)

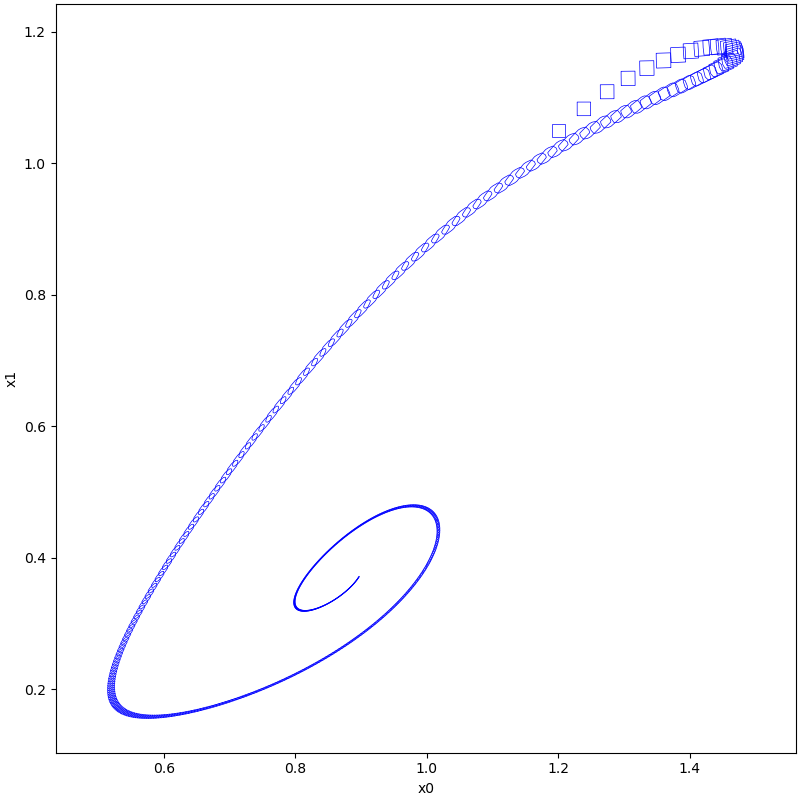
plot(tps, [0, 1])
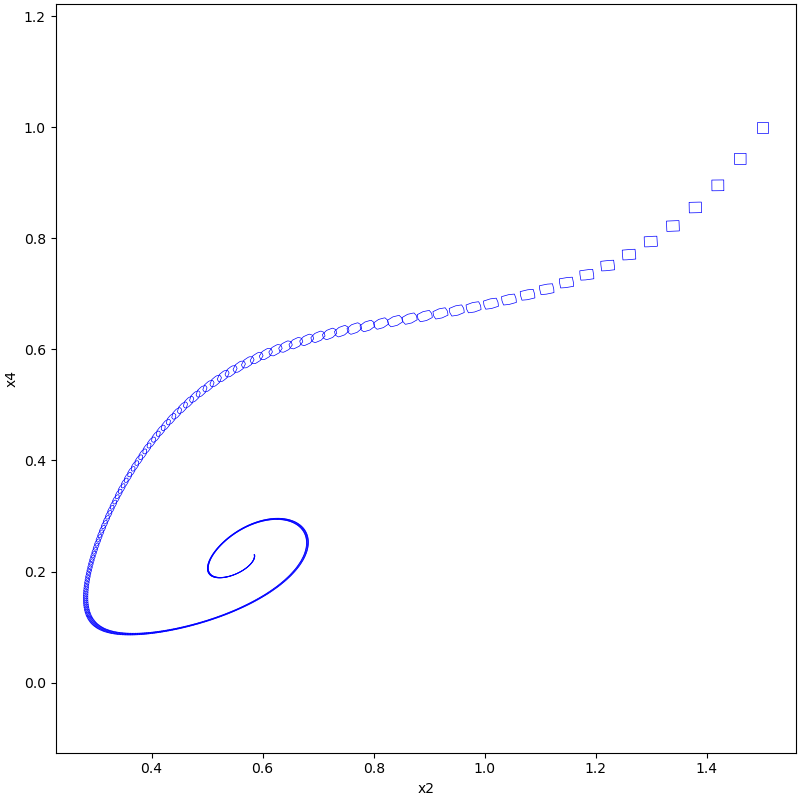
plot(tps, [2, 4])
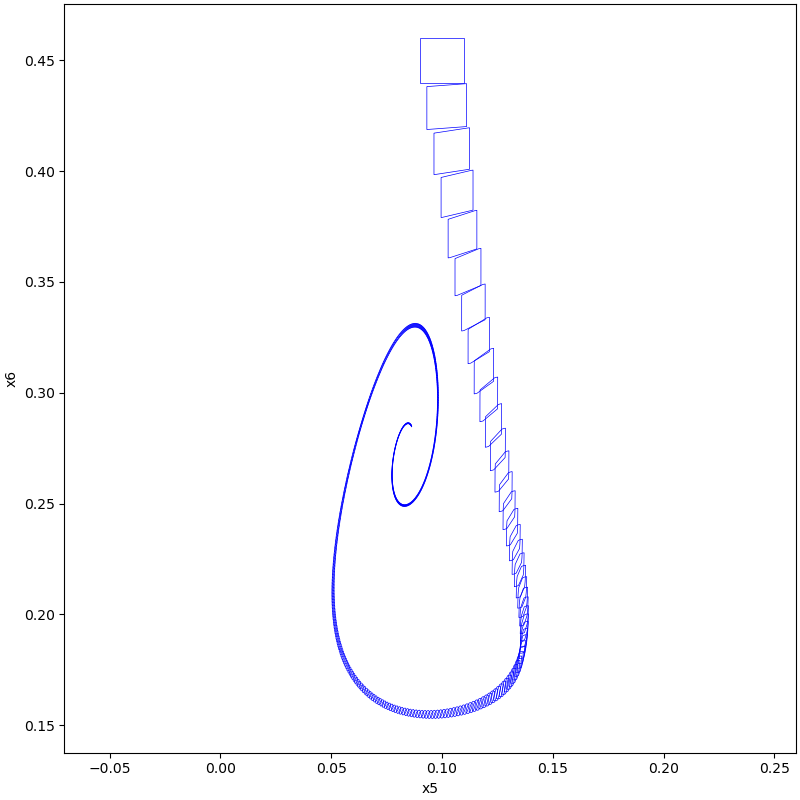
plot(tps, [5, 6])
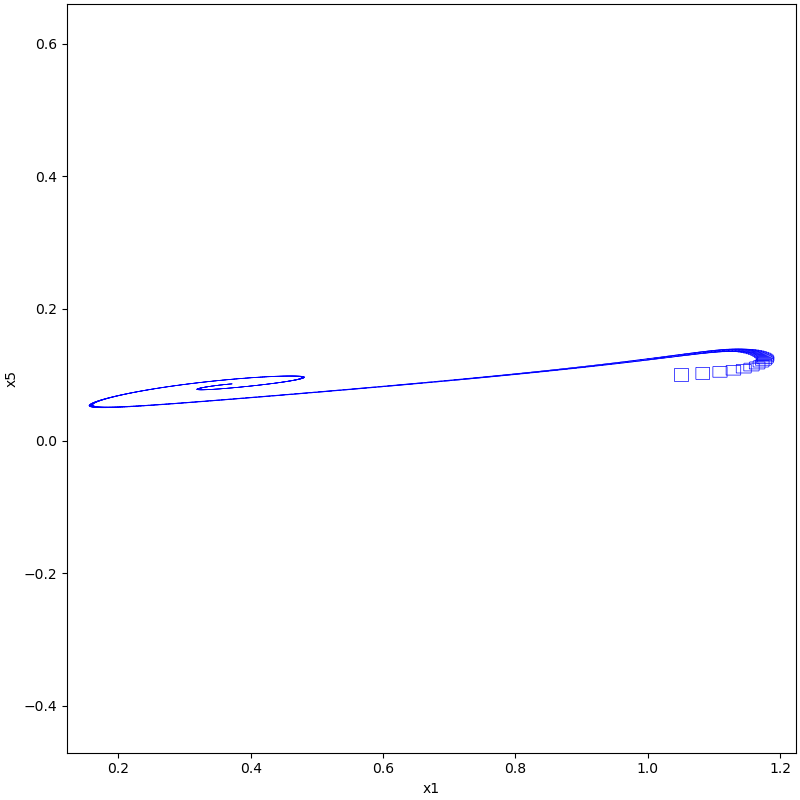
plot(tps, [1, 5])
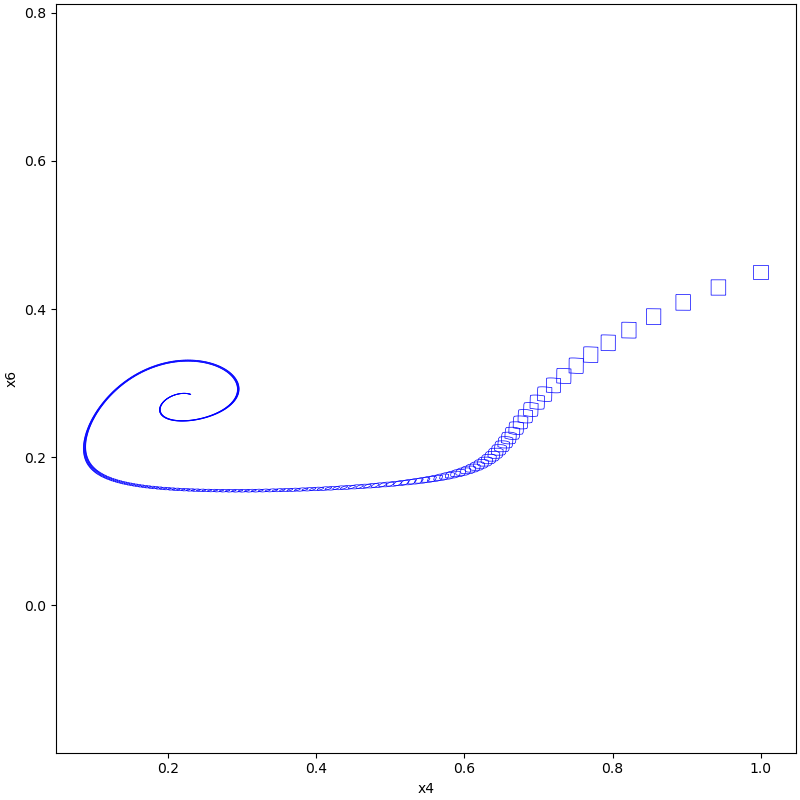
plot(tps, [4, 6])

Results​