Skip to main content

Interval

Definition​

I≔{x∈Rn∣x‾i≤xi≤x‾i,∀i=1,⋯ ,n}{\cal I} \coloneqq \{ x \in \mathbb{R}^n | {\underline{x}}_{i} \leq x_{i} \leq \overline{x}_{i}, \forall i =1, \cdots , n \}
caution

In order to do computation simultaneously for intervals, we use tensor as bounds but a real number in our implementation, this is the difference between the theoretical definition and our real implementation, for more detail, please check our source code.

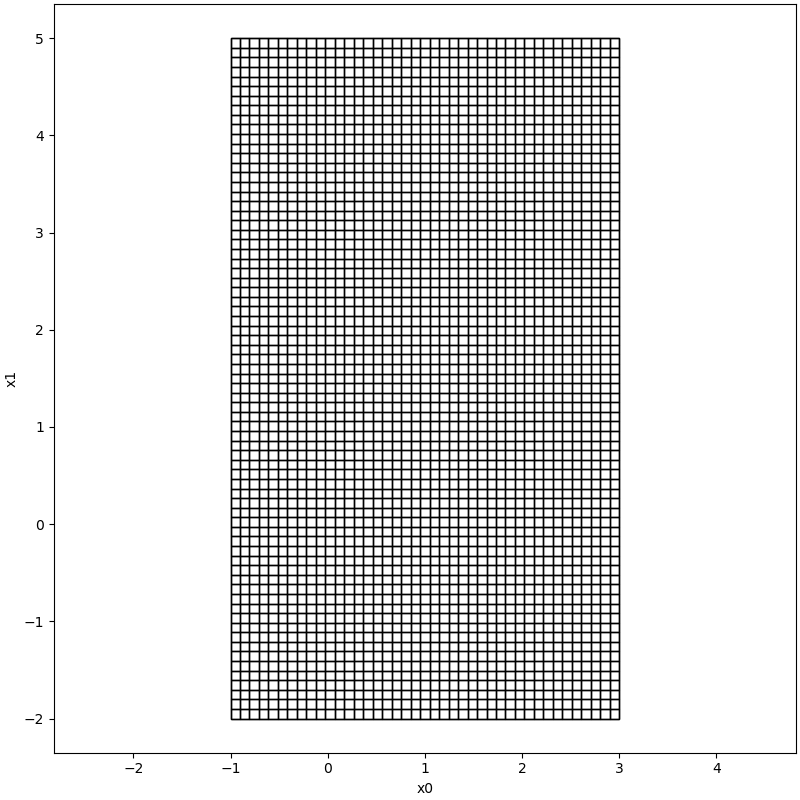
Example​

from pyrat.geoemtry import Interval
from pyrat.util.visualization import plot
from pyrat.geometry import Geometry
from pyrat.geometry.operation import partition

a = Interval([-1,-2],[3,5])
parts = partition(a, 0.1, Geometry.TYPE.INTERVAL)
plot([*parts,a], [0, 1])

Operations​

enclose​

boundary​

Arithmetic​

addition or '+'​

[x]+[y]=[x‾+y‾,x‾+y‾][x] + [y] = [\underline{x} + \underline{y}, \overline{x} + \overline{y}]

subtraction or '-'​

[x]−[y]=[x‾−y‾,x‾−y‾][x] - [y] = [\underline{x} - \overline{y}, \overline{x} - \underline{y}]

multiplication or '*'​

[x]⋅[y]=[min⁡(x‾y‾,x‾y‾,x‾y‾,x‾y‾),max⁡(x‾y‾,x‾y‾,x‾y‾,x‾y‾)][x] \cdot [y] = [ \min{(\underline{x} \underline{y}, \underline{x} \overline{y}, \overline{x} \underline{y}, \overline{x} \overline{y})}, \max{(\underline{x} \underline{y}, \underline{x} \overline{y}, \overline{x} \underline{y}, \overline{x} \overline{y})} ]

division or '/'​

[x]/[y]=[x]⋅(1/[y]),1/[y]={∅if y=[0,0][1/y‾,1/y‾]if 0∉[y][1/y‾,∞[if (y‾=0)∧(y‾>0)]−∞,1/y‾if (y‾<0)∧(y‾=0)]−∞,∞[if (y‾<0)∧(y‾>0)[x]/[y] = [x] \cdot (1/[y]), 1/[y]= \begin{cases} \emptyset & \text{if} \ y = [0,0] \\ [1/\overline{y}, 1/\underline{y}] & \text{if} \ 0 \notin [y] \\ [1/\overline{y}, \infty[ & \text{if} \ (\underline{y}=0) \land (\overline{y}>0) \\ ] - \infty, 1/\underline{y} & \text{if} \ (\underline{y}<0) \land (\overline{y}=0) \\ ] - \infty, \infty[ & \text{if} \ (\underline{y}<0) \land (\overline{y}>0) \end{cases}

power or '**'​

[x]n={[x‾n,x‾n]if (x‾<0)∨(n uneven)[x‾n,x‾n]if (x‾<0)∧(n even)[0,max⁡(∣x‾∣,∣x‾∣)n]if (0∈[x])∧(n even)[x]^n = \begin{cases} [\underline{x}^n,\overline{x}^n] & \text{if} \ (\underline{x} < 0) \lor (n \ \text{uneven})\\ [\overline{x}^n, \underline{x}^n] & \text{if} \ (\overline{x} < 0) \land (n \ \text{even}) \\ [0,\max(|\underline{x}|,|\overline{x}|)^n] & \text{if} \ (0 \in [x]) \land (n \ \text{even}) \end{cases}

where n∈Nn \in \N

absolute or '||'​

∣[x]∣={[∣x‾∣,∣x‾∣]if x‾<0[x‾,x‾]if x‾>0[0,max⁡(∣x‾∣,∣x‾∣)]if 0∈[x]|[x]| =\begin{cases} [|\overline{x}|,|\underline{x}|] & \text{if} \ \overline{x}<0 \\ [\underline{x}, \overline{x}] & \text{if} \ \underline{x}>0 \\ [0,\max(|\underline{x}|,|\overline{x}|)] & \text{if} \ 0 \in [x] \end{cases}

matrix multiplication or '@'​

  • real matrix with interval
(X[Y])ij=∑k=1nXik[Y]kj(X[Y])_{ij} = \sum_{k=1}^{n} X_{ik} [Y]_{kj}
  • interval with real matrix
([X]Y)ij=∑k=1n[X]ikYkj([X]Y)_{ij} = \sum_{k=1}^{n} [X]_{ik} Y_{kj}
  • with another interval matrix
([X][Y])ij=∑k=1n[X]ik[Y]kj([X][Y])_{ij} = \sum_{k=1}^{n} [X]_{ik} [Y]_{kj}

where [X]⊆Ro×n[X] \sube \R^{o \times n} and [Y]⊆Rn×p[Y] \sube \R^{n \times p}

exponential​

e[x]=[ex‾,ex‾]e^{[x]} = [e^{\underline{x}}, e^{\overline{x}}]

log​

log⁡([x])={[log⁡x‾,log⁡x‾]if x‾>0[NaN,log⁡x‾]if (x‾<0)∧(x‾≥0)[NaN,NaN]if x‾<0\log{([x])} = \begin{cases} [\log{\underline{x}}, \log{\overline{x}} ] & \text{if} \ \underline{x}>0 \\ [\mathrm{NaN}, \log{\overline{x}}] & \text{if} \ (\underline{x} < 0) \land (\overline{x} \geq 0) \\ [\mathrm{NaN},\mathrm{NaN}] & \text{if} \ \overline{x} < 0 \end{cases}

sqrt​

[x]={[x‾,x‾]if x‾≥0[NaN,x‾]if (x‾<0)∧(x‾≥0)[NaN,NaN]if x‾<0\sqrt{[x]} =\begin{cases} [\sqrt{\underline{x}},\sqrt{\overline{x}}] & \text{if} \ \underline{x} \geq 0 \\ [\mathrm{NaN}, \sqrt{\overline{x}}] & \text{if} \ (\underline{x} <0 ) \land (\overline{x} \geq 0) \\ [\mathrm{NaN}, \mathrm{NaN}] & \text{if} \ \overline{x}<0 \end{cases}

arcsin​

arcsin⁡([x])={[arcsin⁡(x‾),arcsin⁡(x‾)]if (x‾≥−1)∧(x‾≤1),[arcsin⁡(x‾),NaN]if (x‾∈[−1,1])∧(x‾>1),[NaN,arcsin⁡(x‾)]if (x‾<−1)∧(x‾∈[−1,1]),[NaN,NaN]if (x‾<−1)∧(x‾>1)\arcsin([x])=\begin{cases} [\arcsin(\underline{x}), \arcsin(\overline{x})] & \text{if} \ (\underline{x} \geq -1) \land (\overline{x} \leq 1), \\ [\arcsin(\underline{x}), \mathrm{NaN}] & \text{if} \ (\underline{x} \in [-1,1]) \land (\overline{x} > 1), \\ [\mathrm{NaN}, \arcsin(\overline{x})] & \text{if} \ (\underline{x} < -1) \land (\overline{x} \in [-1,1]), \\ [\mathrm{NaN}, \mathrm{NaN}] & \text{if} \ (\underline{x} < -1) \land (\overline{x} >1) \end{cases}

arccos​

arccos⁡([x])={[arccos⁡(x‾),arccos⁡(x‾)]if (x‾≥−1)∧(x‾≤1),[arccos⁡(x‾),NaN]if (x‾<−1)∧(x‾∈[−1,1]),[NaN,arccos⁡(x‾)]if (x‾∈[−1,1])∧(x‾>1),[NaN,NaN]if(x‾<−1)∧(x‾>1)\arccos([x])=\begin{cases} [\arccos(\overline{x}), \arccos(\underline{x})] & \text{if} \ (\underline{x} \geq -1) \land (\overline{x} \leq 1), \\ [\arccos(\overline{x}), \mathrm{NaN}] & \text{if} \ (\underline{x} < -1) \land (\overline{x} \in [-1,1]), \\ [\mathrm{NaN}, \arccos(\underline{x})] & \text{if} \ (\underline{x} \in [-1,1]) \land (\overline{x} > 1), \\ [\mathrm{NaN}, \mathrm{NaN}] & \text{if} (\underline{x} < -1) \land (\overline{x} >1) \end{cases}

arctan​

arctan⁡([x])=[arctan⁡(x‾),arctan⁡(x‾)]\arctan([x])=[\arctan(\underline{x}), \arctan(\overline{x})]

sinh​

sinh⁡([x])=[sinh⁡(x‾),sinh⁡(x‾)]\sinh([x]) = [\sinh(\underline{x}), \sinh(\overline{x})]

cosh​

cosh⁡([x])={[cosh⁡(x‾),cosh⁡(x‾)]if x‾<0,[1,cosh⁡(max⁡(∣x‾∣,∣x‾∣))]if (x‾≤0)∧(x‾≥0),[cosh⁡(x‾),cosh⁡(x‾)]if x‾>0\cosh([x])=\begin{cases} [\cosh(\overline{x}), \cosh(\underline{x})] & \text{if} \ \overline{x} <0 ,\\ [1, \cosh(\max(|\underline{x}|,|\overline{x}|))] & \text{if} \ (\underline{x} \leq 0) \land (\overline{x} \geq 0), \\ [\cosh(\underline{x}), \cosh(\overline{x})] & \text{if} \ \underline{x} >0 \end{cases}

tanh​

tanh⁡([x])=[tanh⁡(x‾),tanh⁡(x‾)]\tanh([x])=[\tanh(\underline{x}), \tanh(\overline{x})]

arcsinh​

arcsinh([x])=[arcsinh(x‾),arcsinh(x‾)]\mathrm{arcsinh}([x])=[\mathrm{arcsinh}(\underline{x}), \mathrm{arcsinh}(\overline{x})]

arccosh​

arccosh([x])={[arccosh(x‾),arccosh(x‾)]if x‾≥−1,[NaN,arccosh(x‾)]if (x‾<1)∧(x‾≥1),[NaN,NaN]if x‾<1\mathrm{arccosh}([x])= \begin{cases} [\mathrm{arccosh}(\underline{x}), \mathrm{arccosh}(\overline{x})] & \text{if} \ \underline{x} \geq -1,\\ [\mathrm{NaN}, \mathrm{arccosh}(\overline{x})] & \text{if} \ (\underline{x}<1)\land(\overline{x} \geq 1 ), \\ [\mathrm{NaN}, \mathrm{NaN}] & \text{if} \ \overline{x} <1 \end{cases}

arctanh​

arctanh(x)={[arctanh(x‾),arctanh(x‾)]if (x‾>−1)∧(x‾<1),[arctanh(x‾),NaN]if (x‾∈]−1,1[)∧(x‾≥1),[NaN,arctanh(x‾)]if (x‾≤−1)∧(x‾∈]−1,1[),[NaN,NaN]if (x‾≤−1)∧(x‾≥1)\mathrm{arctanh}(x)=\begin{cases} [\mathrm{arctanh}(\underline{x}), \mathrm{arctanh}(\overline{x})] & \text{if} \ (\underline{x}>-1) \land (\overline{x}< 1), \\ [\mathrm{arctanh}(\underline{x}), \mathrm{NaN}] & \text{if} \ (\underline{x} \in ]-1,1[) \land (\overline{x} \geq 1), \\ [\mathrm{NaN}, \mathrm{arctanh}(\overline{x})] & \text{if} \ (\underline{x} \leq -1) \land (\overline{x} \in ]-1,1[), \\ [\mathrm{NaN}, \mathrm{NaN}] & \text{if} \ (\underline{x} \leq -1) \land (\overline{x} \geq 1) \end{cases}

sin​

sin⁡([x])={[−1,1]if (x‾−x‾≥2π)∨(y‾∈R1∧y‾∈R1∧y‾>y‾)∨(y‾∈R1∧y‾∈R3)∨(y‾∈R2∧y‾∈R2∧y‾>y‾)∨(y‾∈R3∧y‾∈R3∧y‾>y‾)[sin⁡(y‾),sin⁡(y‾)]if (y‾∈R1∧y‾∈R1∧y‾≤y‾)∨(y‾∈R3∧y‾∈R3)∨(y‾∈R3∧y‾∈R3∧y‾≤y‾)[min⁡(sin⁡(y‾),sin⁡(y‾)),1]if (y‾∈R1∧y‾∈R2),(y‾∈R3∧y‾∈R2)∨[−1,max⁡(sin⁡(y‾),sin⁡(y‾))]if (y‾∈R2∧y‾∈R1)∨(y‾∈R2∧y‾∈R3),[sin⁡(y‾),sin⁡(y‾)]if (y‾∈R2∧y‾∈R2∧y‾≤y‾)\sin([x])=\begin{cases} [-1,1] & \text{if} \ (\overline{x}-\underline{x} \geq 2\pi) \lor \\ & (\underline{y} \in R_1 \land \overline{y} \in R_1 \land \underline{y} > \overline{y}) \lor \\ & (\underline{y} \in R_1 \land \overline{y} \in R_3) \lor \\ & (\underline{y} \in R_2 \land \overline{y} \in R_2 \land \underline{y} > \overline{y}) \lor \\ & (\underline{y} \in R_3 \land \overline{y} \in R_3 \land \underline{y} > \overline{y}) \\ [\sin(\underline{y}), \sin(\overline{y})] & \text{if} \ (\underline{y} \in R_1 \land \overline{y} \in R_1 \land \underline{y} \leq \overline{y}) \lor \\ & (\underline{y} \in R_3 \land \overline{y} \in R_3) \lor \\ & (\underline{y} \in R_3 \land \overline{y} \in R_3 \land \underline{y} \leq \overline{y}) \\ [\min(\sin(\underline{y}),\sin(\overline{y})),1] & \text{if} \ (\underline{y} \in R_1 \land \overline{y} \in R_2), \\ & (\underline{y} \in R_3 \land \overline{y} \in R_2) \lor \\ [-1,\max(\sin(\underline{y}),\sin(\overline{y}))] & \text{if} \ (\underline{y} \in R_2 \land \overline{y} \in R_1) \lor \\ & (\underline{y} \in R_2 \land \overline{y} \in R_3), \\ [\sin(\overline{y}),\sin(\underline{y})] & \text{if} \ (\underline{y} \in R_2 \land \overline{y} \in R_2 \land \underline{y} \leq \overline{y}) \end{cases}

where R1=[0,π2[,R2=[π2,3π2[,R3=[3π2,2π[,y‾=mod(x‾,2π),y‾=mod(x‾,2π)R_1=[0,\frac{\pi}{2}[, R_2=[\frac{\pi}{2},\frac{3\pi}{2}[, R_3=[\frac{3\pi}{2}, 2\pi[, \underline{y}=\mathrm{mod}(\underline{x},2\pi), \overline{y}=\mathrm{mod}(\overline{x},2\pi)

cos​

cos⁡([x])={[−1,1]if (x‾−x‾≥2π)∨(y‾∈R1∧y‾∈R1∧y‾>y‾)∨(y‾∈R2∧y‾∈R2∧y‾>y‾),[cos⁡(y‾),cos⁡(y‾)]if (y‾∈R2∧y‾∈R2∧y‾≤y‾),[min⁡(cos⁡(y‾),cos⁡(y‾)),1]if (y‾∈R2∧y‾∈R1),[−1,max⁡(cos⁡(y‾),cos⁡(y‾))]if (y‾∈R1∧y‾∈R2),[cos⁡(y‾),cos⁡(y‾)]if (y‾∈R1∧y‾∈R1∧y‾≤y‾)\cos([x])=\begin{cases} [-1,1] & \text{if} \ (\overline{x} - \underline{x} \geq 2 \pi) \lor \\ & (\underline{y} \in R_1 \land \overline{y} \in R_1 \land \underline{y} > \overline{y}) \lor \\ & (\underline{y} \in R_2 \land \overline{y} \in R_2 \land \underline{y} > \overline{y}),\\ [\cos(\underline{y}), \cos(\overline{y})] & \text{if} \ (\underline{y} \in R_2 \land \overline{y} \in R_2 \land \underline{y} \leq \overline{y}), \\ [\min(\cos(\underline{y}),\cos(\overline{y})),1] & \text{if} \ (\underline{y} \in R_2 \land \overline{y} \in R_1), \\ [-1,\max(\cos(\underline{y}),\cos(\overline{y}))] & \text{if} \ (\underline{y} \in R_1 \land \overline{y} \in R_2), \\ [\cos(\overline{y}), \cos(\underline{y})] & \text{if} \ (\underline{y} \in R_1 \land \overline{y} \in R_1 \land \overline{y} \leq \overline{y}) \end{cases}

where R1=[0,π[,R2=[π,2π[,y‾=mod(x‾,2π),y‾=mod(x‾,2π)R_1=[0,\pi[, R_2=[\pi,2\pi[, \underline{y}=\mathrm{mod}(\underline{x},2\pi), \overline{y}=\mathrm{mod}( \overline{x},2\pi)

###tan

tan⁡([x])={]−∞,∞[if (x‾−x‾≥π)∧(z‾∈R1∧z‾∈R1∧z‾>z‾)∨(z‾∈R2∧z‾∈R2∧z‾>z‾)∨(z‾∈R1∧z‾∈R2),[tan⁡(z‾),tan⁡(z‾)]if (z‾∈R1∧z‾∈R1∧z‾∈z‾)∨(z‾∈R2∧z‾∈R2∧z‾∈z‾)\tan([x])=\begin{cases} ]-\infty,\infty[ & \text{if} \ (\overline{x}-\underline{x} \geq \pi) \land \\ & (\underline{z} \in R_1 \land \overline{z} \in R_1 \land \underline{z} > \overline{z}) \lor \\ & (\underline{z} \in R_2 \land \overline{z} \in R_2 \land \underline{z} > \overline{z}) \lor \\ & (\underline{z} \in R_1 \land \overline{z} \in R_2), \\ [\tan(\underline{z}),\tan(\overline{z})] & \text{if} \ (\underline{z} \in R_1 \land \overline{z} \in R_1 \land \underline{z} \in \overline{z}) \lor \\ & (\underline{z} \in R_2 \land \overline{z} \in R_2 \land \underline{z} \in \overline{z}) \end{cases}

where R1=[0,π2[,R2=[π2,π[,z‾=mod(x‾,π),z‾=mod(x‾,π)R_1=[0,\frac{\pi}{2}[, R_2=[\frac{\pi}{2}, \pi[, \underline{z}=\mathrm{mod}(\underline{x},\pi), \overline{z}=\mathrm{mod}(\overline{x},\pi)

cot​

cot⁡([x])={]−∞,∞[if (x‾−x‾≥π)∨(z‾>z‾),[cot⁡(z‾),cot⁡(z‾)]if (z‾≤z‾)\cot([x]) = \begin{cases} ]-\infty,\infty[ & \text{if} \ (\overline{x}-\underline{x} \geq \pi) \lor (\underline{z} > \overline{z}), \\ [\cot(\overline{z}), \cot(\underline{z})] & \text{if} \ (\underline{z} \leq \overline{z}) \end{cases}

where z‾=mod(x‾,π),z‾=mod(x‾,π)\underline{z}=\mathrm{mod}(\underline{x},\pi),\overline{z}=\mathrm{mod}(\overline{x},\pi)

References​

[1] Althoff, M., & Grebenyuk, D. (2016). Implementation of interval arithmetic in {CORA} 2016. In Proc. of the 3rd International Workshop on Applied Verification for Continuous and Hybrid Systems (pp. 91-105).

[2]: Wikipedia contributors. (2022, May 5). Interval arithmetic. In Wikipedia, The Free Encyclopedia. Retrieved 08:05, June 9, 2022, from https://en.wikipedia.org/w/index.php?title=Interval_arithmetic&oldid=1086274354

[3]: Rump, S. M. (1999). Fast and parallel interval arithmetic. BIT Numerical Mathematics, 39(3), 534-554.

[4]: Moore, R. E., Kearfott, R. B., & Cloud, M. J. (2009). Introduction to interval analysis. Society for Industrial and Applied Mathematics.

[5]: Shary, S. P. (2019). Numerical computation of formal solutions to interval linear systems of equations. arXiv preprint arXiv:1903.10272.