Skip to main content

Polytope

Definition​

H-Representation​

P≔{x∈Rn∣Cx≤d},C∈Rq×n,d∈Rq{\cal P} \coloneqq \{ x \in \mathbb{R}^{n} | Cx \leq d\}, C \in \mathbb{R}^{q \times n}, d \in \mathbb{R}^{q}

V-Representation​

P≔{∑i=1rαivi∣αi∈R,αi≥0,∑i=1rαi=1}{\cal P} \coloneqq \{ \sum_{i=1}^{r} {\alpha}_{i} v^{i} | {\alpha}_{i} \in \mathbb{R}, {\alpha}_{i} \geq 0, \sum_{i=1}^{r} {\alpha}_{i} =1 \}

Example​

import numpy as np

from pyrat.geometry import Polytope, Geometry
from pyrat.geometry.operation import cvt2
from pyrat.util.visualization import plot

# initial from linearly ineqalities Ax <= b
a = np.array(
    [
        [-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1],
        [1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1],
        [1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0],
        [0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0],
        [0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1],
    ]
)
b = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 1, 2, 2, 1, 2, 3])
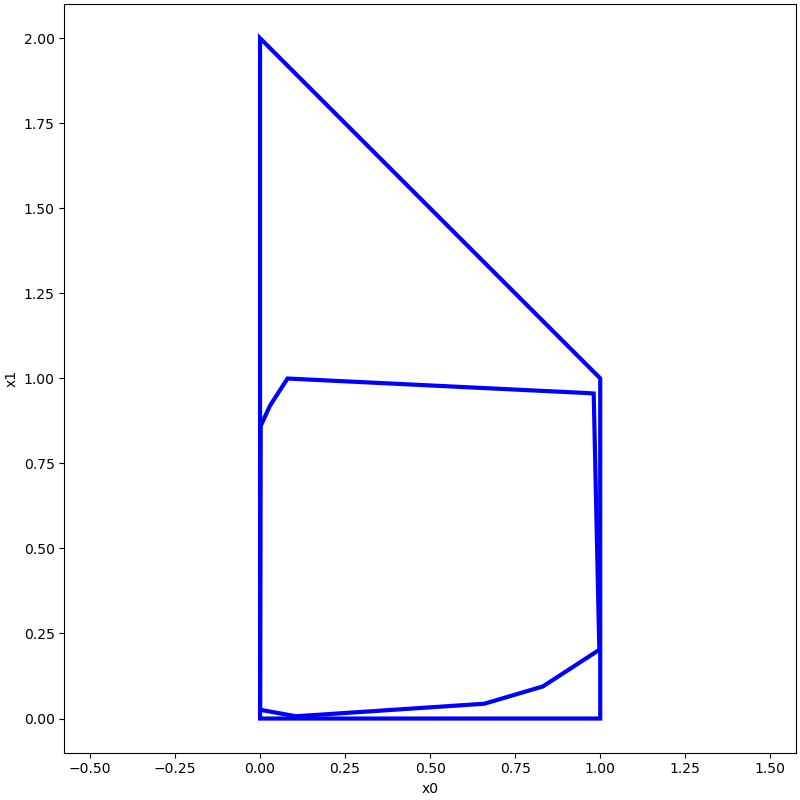
p_from_inequalities = Polytope(a, b)

points=np.random.rand(100,2)
p_from_vertices=cvt2(points,Geometry.TYPE.POLYTOPE)

plot([p_from_inequalities,p_from_vertices], [0, 1])

Operations​

enclose​

boundary​

Arithmetic​

scalar operations​

addition or '+'
subtraction or '-'
multiplication or '*'
division or '/'
matrix multiplication or '@'

References​